If you are a market researcher, and you want to make sure that you get more reliable results for a subgroup in a survey, what do you do? You must increase the overall sample size (and spend a lot of money), right?
Actually, you don’t.
You can oversample that group only, and then weight it down to its known proportion in the population. For example, you may want to increase the number of managers and decrease the number of housewives (because the former are usually more heterogeneous than the latter). Oversampling is a common research method, and a very cost-effective way to get precise estimates for a subgroup.
This is a real-world solution, and if we have finite resources to solve a real-world problem, resource allocation must be part of the equation. Higher variability usually demands for more resources.
Why is this relevant in a blog about charts and information visualization? Glad you ask.
The Great Irregular Interval Debate
Let me give you an example. A while back, Jon Peltier wrote in his blog:
I don’t understand the obsession with an equal date interval. A line chart need not show the trend of only evenly-spaced data. Suppose I am observing temperatures, and I decide for simplicity that where the temperature hasn’t changed, or where it has been changing steadily, I do not need to record every value. Overnight after the temperature has dropped, I can characterize my temperature profile with one point per hour. As the sun rises, I may need more frequent recordings to capture the morning warm up. Then the clouds blow over, it starts to rain, then it clears up again; I may need minute-by-minute data points to track this. When I make my plot, is it any less relevant because the spacing of the data ranges from minutes to hours?
This is oversampling, and a wise resource allocation, too. In a survey, you weight the subgroup down to its right proportion, and that’s also what you do in a chart, when irregular date intervals are displayed proportionally.
Stephen Few disagrees:
Using a line to connect values along unequal intervals of time or to connect intervals that are not adjacent in time is misleading.
Furthermore:
How could we trust graphical representations of time series or frequency distributions if their shapes could have been altered by inconsistently manipulating the sizes of intervals along the scale, either arbitrarily or intentionally to deceive? We can derive meaning from patterns and trends that these graphs display only if the intervals are consistent.
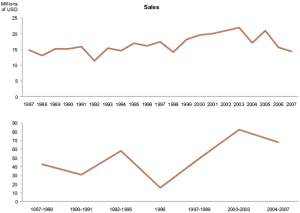 He exemplifies his argument with these two charts (actually, there are three, but we can safely disregard the third one).
He exemplifies his argument with these two charts (actually, there are three, but we can safely disregard the third one).
The first chart displays the correct annual sales. The second one displays arbitrarily grouped annual sales and, obviously, its pattern is quite different.
Now, the second chart is plain wrong, so I am not sure if you can use it to argue against unequal intervals.
Let’s use a fairer example with the same dataset and the same arbitrary grouping.
Compare the orange line with Few’s first chart. I actually don’t see much difference. Sure you lose a lot of detail, but the basic pattern is there. Instead of sums, I am using averages (you can’t compare a single year with the total sales of three or four years).
The other two lines show the difference between equal and unequal intervals. The brown line displays the data points unequally spaced while the gray one uses equal intervals (Few’s second chart). I had to make some assumptions regarding the reference date, so this is not the best example, but it is good enough to show the potential risk of using equal intervals with unequal intervals of time.
Bottom line, oversampling is a useful method for better resource allocation. We can view irregular time series as some sort of oversampling, provided there are no missing values and irregular intervals in the chart are consistent with intervals in the time series.
Grouping data points is always a tricky issue, and Stephen Few show it clearly, but we shouldn’t infer that “line graphs and irregular intervals is an incompatible partnership.”
(When using time series in Excel, make sure that category axis labels are recognized as dates. Alternatively, use a scatter plot with connected data points.)

The above question is what the issue really is about: trust in the truthfulness of a chart. If you have a good reason to use irregular intervals then use them only if you also make perfectly clear what you do in creating your chart and why. Without such kind of ‘full disclosure’ your readers simply can’t trust your chart. Also, you could also give thought to rearranging your irregular data to fit regular intervals (for example by interpolating where necessary and clearly marking which data points are real and which are derived).
@nixnut: there are many ways to deceive with charts, and the arbitrary use of irregular intervals is one of them. But we can’t stop using a chart format just because some people use it the wrong way. “Full-disclosure” should always be there by design, but some redundancy may be needed in such cases.
In science: if you are plotting observations/measurements (e.g. temperature), and the data plotted is exactly the data taken, then you are being completely honest about the “plot”. Also, typically, to be taken seriously, you have an obligation to assess and describe the sources of error in the entire measurement system.
In business: taking measurements is usually much more arbitrary and the context and purpose is crucial though typically obscure (I work in a LARGE corporation). Attempting to investigate and assess the sources of error is often difficult, time consuming, and may be opposed by those who own the “measurement” systems/data sources (among others!).
Worse, the people who ask for a report may want it in the morning but have gone home, so it can be difficult to be sure what they want to know. (I have found that a big source of error is simply the meaning of words commonly used. I once tried to make a list of all the ways the term “cost” was used in my area, and quickly gave up. The implications for people creating and marketing dashboards in their organizations are significant. )
In my job, a major source of time uncertainty is that, of necessity, systems produce data that is consumed by other systems that in turn feed others. Some of it may be entered by hand, and people can be inconsistent in getting that bit of their job done. So there can be many different (and inconsistent) lags involved in piecing together a report. In such circumstances, getting equal time intervals, much less an accurate picture of even simple data, is sometimes a bit of a struggle!
As far as “inconsistently manipulating the sizes of intervals”, that is simply fraud, and sounds like Few is addressing a somewhat different topic, yes?
Jorge-
Not related to this post, but I’m pretty sure you could find some use for this dilbert cartoon http://dilbert.com/strips/comic/2009-03-07/
Recording temperature is a very different case that what John’s stamp chart shows. The stamp measurements are not observations; they are the dates at which the price of stamps changed and the time in days until the next change. Necessarily, they are not equal intervals.
John’s x-axis (1st chart) does have equal intervals: 22 months. It’s a strange interval, but it is equal. The data are plotted correctly – the date at which the price change occurred.
Stephen’s criticism is connecting the measurements with a line. The truth is, you don’t know what happened between most measurements. Implying that the movement from one point to the next is gradual is misleading.
John recognizes this and his solution is the Step Chart (2nd chart). In the case of the stamp prices, you do know what happened to price between the dates: nothing. I think the step chart is completely appropriate.
Very misleading are time series charts where the x-axis is categorical but is implied as being continuous, like the second chart in Stephen’s newsletter article (x-axis of 1997, 1998, 2000). But this is not what John did.
Jonah: “Implying that the movement from one point to the next is gradual is misleading.” You are right, but with continuous data we must find the right balance between level of detail and the data we need to answer a specific question. Using line charts to display Nasdaq at close or decennial census data could be misleading because we are assuming a non-existent graduality, but how can we ever use a line chart if we can’t accept this trade-off?
@Jorge
I think some of my comment was ambiguous. When I wrote, “what happened between most measurements” I was referring to missing measurements, not the time within an interval during which there are no measurements.
Agreed, balance is the key. For any continuous variable, you have to ask if smaller intervals would change the signal or just introduce noise. You’re completely right, the trade-off is required for any chart of continuous data.
You got me thinking though. Is Nasdaq value at close really continuous? Nasdaq value during market hours is continuous. With unequal interval observations you would definitely have a continuous function. But if you rigidly define the interval, does that change the problem? If so, does that add more importance for Stephen’s argument in favor of equal intervals?
Maybe the Nasdaq example is confusing. Is there a difference (of problem attributes, not actual values) between the questions of, “How many people are in an office building at any one time today?” and, “How many people showed up to work today?”