So, this data visualization thing is new to you, but you already know enough to avoid basic mistakes (pies, 3D…). While playing with the data, you make these two charts:

You already know that a bar chart helps you to compare data points, while a line chart is better at displaying trends, right? But you keep staring at them, not knowing which one to choose. Suddenly, your little guardian angel whispers: “the bar chart is wrong”.
The bar chart? What’s wrong with the bar chart? And why is the line chart OK?
Then you realize that the vertical scale starts at 30, and apparently it should start at zero, so you change it in both charts:

That leaves a lot of white space under the line. The experts say you don’t have to start scales at zero if you are using line charts. So you revert the changes in the line chart:
Ah, yes! Now you can choose one of them. Your guardian angel agrees that both charts are correct. So, do it, pick one!
What’s the problem? Is there something bothering you?
Humm, I see. They don’t look that similar. You believe that people may draw different conclusions depending on the chart you choose.
OK, let’s discuss this a bit. Let’s talk about resolution.
What is chart resolution, anyway?
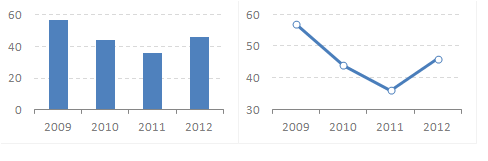
Higher resolution is usually a good thing. It means that you can see more clearly the difference between data points. To improve resolution in a chart, you zoom in, using the numeric scales:
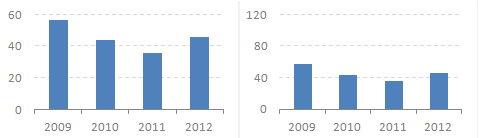
How much you can zoom in? Well, the lower limit should be the first nice round number below the minimum value in your data set, and the upper limit should be (you’ve guess it) the first nice round number above the maximum value.
You have to make a little change to the rule when it comes to bar charts. In a bar chart, people compare heights, so if the bars are not proportional to the data they encode, you are misleading your audience. So, the charts above are both correct, but the one below is not:
That’s why the lower limit in a bar chart should always be the value that maintains the right proportions (usually zero). So, the take-away message is, improve resolution byt changing the scale, but in a bar chart you must keep proportions aligned with the data.
What about slopes?
Line charts are more subtle. Both charts below are correct:
The only difference between them is that the one on the left has a higher resolution, and in general is a better option considering Cleveland’s suggestions for banking to 45º (slopes should average around 45º). You can do it by changing the numeric scales and/or the chart aspect ratio. This is a suggestion (an excellent suggestion), but it also tells you that there is no strict rule to obey.
To be completely honest, I don’t care much about scales or aspect ratio in line charts, as long as they do not go overboard. What really matters is to have something to compare with. In the post Weltanschauung, Lies and Charts, I use these politically biased charts…

… and argue that only when you have more than one series you can learn anything from a line chart, like this:

So it doesn’t matter much what you do with scales or aspect ratio, as long as you have two or more series and your goal is to compare them.
You can learn more about scales in Naomi Robbin’s Creating More Effective Graphs and she often writes about it, like in here and here.
Perhaps you could use this as a rule of thumb: use a bar chart when you have a single series and a line chart when you have two or more series. It will not always work, but it’s a good starting point, don’t you think?
By the way: “méfiez-vous des morceaux choisis” is a lovely French expression that roughly translates to “beware of selected pieces”.


I don’t subscribe to changing the vertical axis to exaggerate gradients or gradient changes.
Whenever I see a chart which doesn’t start at Zero I suspect that someone is manipulating the story for there own benefit.
Vertical axis should always start at 0, unless you have negative numbers. That way the reader can see what percentage the values are of the whole a lot easier than without having the 0 in the axis.
But then you know what they say, Sex, Lies and Statistics…
There are some cases (like the pH scale) where zero is meaningless (most of the time) while small differences are important. Like everything in life, the key is to find the right balance and do not assume that a one-size-fits-all approach make things simpler.
If you want to lie, nothing can stop you. You can lie with words, you can lie with numbers, you can lie with charts. It’s not the medium, is the messenger…
Thanks for posting this! It’s hugely useful to see such a concise visual case study of two such popular charts.
Another resource worth mentioning in this context is Zacks and Tversky’s “Bars and Lines: A Study of Graphic Communication” (linked here). The authors present a series of experiments evaluating the differences in how people read bar charts and line graphs.
Another potential concern when choosing between a bar and a line chart is: Does the interpolation of connecting the dots with a line convey a misleading message?
Sometimes data is just a snapshot, eg last value in a time period, while this can be useful for getting a quick overview, using a line chart may convey information that is not an accurate representation, eg hiding variation.
The resolution of the horizontal axis should be considered as well.
There may be approaches to add this missing information to the view depending on the situation, eg range bars.
I’m with Joe on interpolation…
To me, it looks like the two plots introduced here show different data, since the x-axis is time, which is continuous. I’m guessing that the bar chart is supposed to convey values that are averaged or totaled across the whole year, though if that was the case it’d be nice if there was no gap between the bars, just as there is no gap between years. But the line plot clearly connects a series of points in x-y space… those points are some sort of data associated with mid-year. By connecting the dots, the plot suggests that halfway between data points a best guess is that the value would be about halfway in-between.
A nice example where connecting the dots would be inappropriate is if the values were arctic sea-ice extent. The points could be right, but sea ice is far more extensive in late december than it is in mid-summer, so interpolating with a straight line is not accurate.
To expand on Jorge’s comment, all logarithmic scales (pH, earthquake magnitude, sound decibles, etc.) are not rooted in zero. I can see Hui’s point applying to all linear scales, but I do think there are good exceptions to this rule.
I thunk it is a good practice if we draw the readers attention to the fact that the scale does not start from zero [for a line chart] to improve resolution. Maybe a picture in picture technique should be used with the non-zero graph being the main / bigger graph and the zero graph being an inset.
Jorge,
As usual, another great post.
There is data purist attitude that I don’t agree with. Changing something like the Y scale on a graph to show resolution is one of those no no’s for the data purist that will have them up in arms. In all but a few cases, I think that school of thought misses the point of charts.
The point, (to me) of a great chart is that it conveys a point. To me, the difference between Chart A and Chart B is not whether B is more correct than A, it’s what is the point the author is trying to convey. In chart A, the point is that the federal tax rate for the wealthiest 1% has really come down a lot, so it would not be so bad to put it up a littly bit. In Chart A, it makes the point (less well) that the tax rate shouldn’t change.
One note here about banking to 45 degrees, this is good practice for a single chart, but too often I see two or more plots side by side where each plot is banked. Changing the scales for each plot prevents comparison of slopes among the charts.